Have you ever wondered what the square root of 10000 is and why it matters? The square root of 10000 is a fundamental mathematical concept that plays a significant role in various fields, from engineering to finance. Understanding this concept not only sharpens your math skills but also provides valuable insights into problem-solving in real-life scenarios. Whether you're a student, professional, or simply someone curious about math, this article will guide you through everything you need to know about the square root of 10000.
The square root of 10000 is a perfect square, meaning it has an exact integer value. This makes it an excellent example for learning about square roots and their applications. In this article, we will explore the definition of square roots, how to calculate them, and why the square root of 10000 is particularly significant. By the end of this guide, you'll have a clear understanding of this concept and its relevance in various domains.
From its historical importance in mathematics to its modern-day applications in technology and finance, the square root of 10000 is more than just a number. It represents a bridge between theoretical math and practical problem-solving. Let’s dive deeper into this fascinating topic and uncover its many layers.
Read also:Unveiling The Truth Behind The Subhashree Mms Video Controversy
Table of Contents
- What is a Square Root?
- How to Calculate the Square Root of 10000
- Significance of the Square Root of 10000
- Practical Applications of Square Roots
- Historical Perspective on Square Roots
- Common Misconceptions About Square Roots
- Mathematical Properties of the Square Root of 10000
- Tools and Calculators for Finding Square Roots
- Step-by-Step Examples of Square Root Calculations
- Conclusion
What is a Square Root?
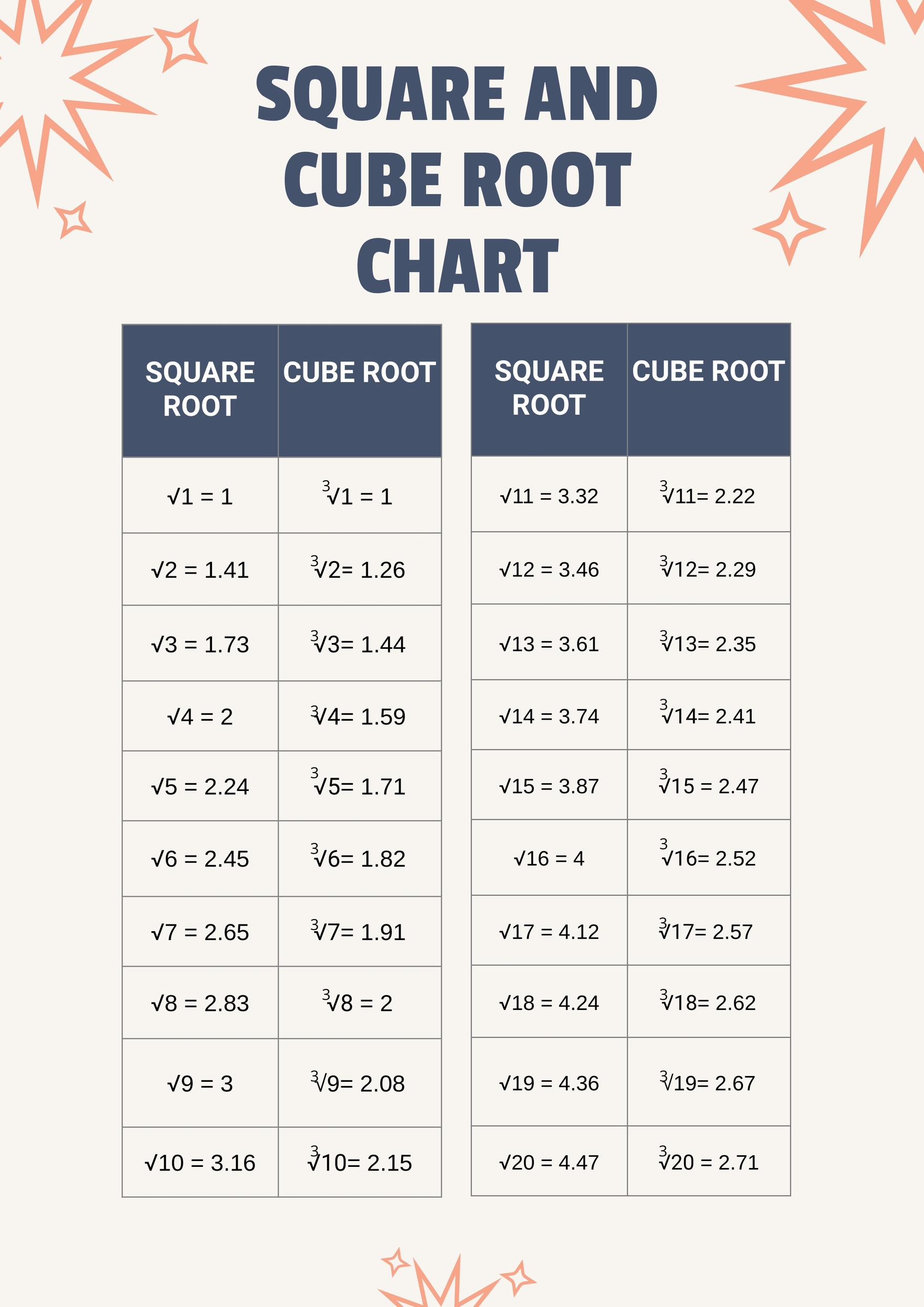
A square root is a mathematical operation that determines a number which, when multiplied by itself, produces the original number. For example, the square root of 10000 is 100 because 100 multiplied by 100 equals 10000. The symbol used to denote a square root is √, so the square root of 10000 can be written as √10000.
The concept of square roots has been around for centuries and forms the foundation of many mathematical principles. It is particularly important in algebra, geometry, and calculus. Understanding square roots helps in solving equations, calculating areas, and even determining distances.
Why Are Square Roots Important?
- They are essential for solving quadratic equations.
- Square roots are used in geometry to calculate the length of sides in squares and triangles.
- They are fundamental in advanced mathematical operations like logarithms and exponents.
How to Calculate the Square Root of 10000
Calculating the square root of 10000 is relatively straightforward because it is a perfect square. A perfect square is a number that can be expressed as the product of an integer multiplied by itself. In this case, 100 × 100 equals 10000, so the square root of 10000 is 100.
Methods to Calculate Square Roots
While the square root of 10000 is simple to calculate, there are several methods to find square roots for numbers that are not perfect squares. Below are some commonly used techniques:
- Prime Factorization: Break the number down into its prime factors and group them into pairs to find the square root.
- Long Division Method: A manual method to find the square root of any number, especially useful for non-perfect squares.
- Using a Calculator: Modern calculators and digital tools can instantly compute square roots.
Significance of the Square Root of 10000
The square root of 10000 holds special significance because it is a perfect square. Perfect squares are numbers that result from multiplying an integer by itself, and they are often used as benchmarks in mathematical calculations. The square root of 10000, which is 100, is frequently used in real-life applications such as:
- Calculating areas of squares with side lengths of 100 units.
- Financial calculations involving percentages and interest rates.
- Engineering designs that require precise measurements.
Why is 10000 a Perfect Square?
The number 10000 is a perfect square because it can be expressed as 100 × 100. This property makes it an ideal example for teaching and learning about square roots. Understanding perfect squares helps in simplifying complex mathematical problems and improving computational efficiency.
Read also:Comprehensive Guide To Understanding And Mastering Keyword
Practical Applications of Square Roots
Square roots are not just theoretical concepts; they have numerous practical applications in various fields. Below are some examples of how the square root of 10000 and other square roots are used in real life:
1. Engineering and Architecture
In engineering, square roots are used to calculate distances, areas, and dimensions. For instance, if an architect needs to design a square plot with an area of 10000 square meters, the side length of the square would be the square root of 10000, which is 100 meters.
2. Finance and Economics
Square roots are used in financial formulas, such as calculating standard deviations in statistics, which are essential for risk assessment in investments. The square root of 10000 might appear in calculations involving percentages or growth rates.
3. Physics and Technology
In physics, square roots are used in formulas related to velocity, acceleration, and energy. For example, the square root of 10000 could represent the magnitude of a vector in a two-dimensional space.
Historical Perspective on Square Roots
The concept of square roots dates back to ancient civilizations. The Babylonians and Egyptians were among the first to explore square roots, using them for practical purposes such as land measurement and construction. Over time, mathematicians like Pythagoras and Euclid further developed the theory of square roots, laying the groundwork for modern mathematics.
Evolution of Square Root Calculations
Before the invention of calculators, mathematicians relied on manual methods like the Babylonian method and long division to calculate square roots. These methods were time-consuming but effective, and they remain valuable for understanding the underlying principles of square roots.
Common Misconceptions About Square Roots
Despite their importance, square roots are often misunderstood. Here are some common misconceptions and the truth behind them:
1. Square Roots Always Produce Positive Numbers
While the principal square root of a number is always positive, every positive number actually has two square roots: one positive and one negative. For example, the square roots of 10000 are +100 and -100.
2. Only Perfect Squares Have Square Roots
All positive numbers have square roots, but only perfect squares have integer square roots. For example, the square root of 2 is approximately 1.414, which is not an integer.
3. Square Roots Are Only Useful in Math
Square roots have applications in various fields, including science, engineering, and finance, making them relevant beyond mathematics.
Mathematical Properties of the Square Root of 10000
The square root of 10000 exhibits several interesting mathematical properties. Below are some key characteristics:
1. Commutative Property
The square root operation is commutative with multiplication. For example, √(100 × 100) = √10000 = 100.
2. Distributive Property
The square root of a product is equal to the product of the square roots. For example, √(100 × 100) = √100 × √100 = 10 × 10 = 100.
3. Relationship with Exponents
The square root of a number can also be expressed as that number raised to the power of 1/2. For example, √10000 = 10000^(1/2) = 100.
Tools and Calculators for Finding Square Roots
In today’s digital age, there are numerous tools and calculators available to help you find square roots quickly and accurately. Some popular options include:
- Scientific Calculators: These devices have dedicated square root functions.
- Online Calculators: Websites like Wolfram Alpha and Desmos offer free square root calculators.
- Mobile Apps: Many math apps provide square root calculations as part of their functionality.
How to Use a Square Root Calculator
Using a square root calculator is simple. Enter the number you want to find the square root of, press the square root button, and the calculator will display the result. For example, entering 10000 will yield 100.
Step-by-Step Examples of Square Root Calculations
To solidify your understanding of square roots, let’s walk through a few examples:
Example 1: Finding the Square Root of 10000
- Identify the number: 10000.
- Determine if it is a perfect square: Yes, 100 × 100 = 10000.
- Write the square root: √10000 = 100.
Example 2: Finding the Square Root of 144
- Identify the number: 144.
- Determine if it is a perfect square: Yes, 12 × 12 = 144.
- Write the square root: √144 = 12.
Example 3: Finding the Square Root of 50 (Non-Perfect Square)
- Identify the number: 50.
- Determine if it is a perfect square: No.
- Use a calculator or estimation: √50 ≈ 7.071.
Conclusion
The square root of 10000 is a fascinating mathematical concept with wide-ranging applications. As a perfect square, it serves as an excellent example for learning about square roots and their significance. From its historical roots to its modern-day uses in science, engineering, and finance, the square root of 10000 demonstrates the power of mathematics in solving real-world problems.
We hope this guide has provided you with a comprehensive understanding of the square root of 10000 and its importance. Whether you're a student, professional, or math enthusiast, mastering this concept can enhance your problem-solving skills and broaden your knowledge. If you found this article helpful, feel free to leave a comment, share it with others, or explore more of our content on mathematics and related topics.